 | ||||
|
1. Cada año la Samltown Optometry Clinic Vende 10,000 armazones para lentes la clínica pide las armazones a un abastecedor regional, que cobre 14 dólares por armazón. Cada pedido incurre en un costo de 50 dólares.
La óptica cree que se demanda de armazones puede acumularse y que el costo por carecer de un armazón durante un año es 15 dólares debido a la pérdida de negocios futuros. El costo anual por mantener un inventario es de 30 centavos por dólar del valor del inventario. ¿Cuál es la cantidad óptima de pedido? ¿Cuál es la escasez máxima que se presentará? ¿Cuál es el nivel máximo de inventario que se presentará?
Solución:
Paso 1: Identifico Modelo
Tamaño Económico de lote reabastecimiento instantáneo con faltantes permitidos ( modelo con escasez)
Paso 2: Determino los costos
Precio del inventario = $15 por armazón
C3=$50 por pedido
C2=$15 unidad/año
C1=$0.30 por dólar del valor del inventario
Entonces el costo 1 corresponde A
$30 --------- $1
x ----------- $15
$0.30/$1 * $15 = $4.50 o simplemente
C1=0.30 * valor del inventario = 0.30(15) = $4.50
Por lo tanto C1=$4.50
La demanda es de r=10,000 armazones al año.
Paso 3: Introducir datos en las formulas
Para Q* (cantidad optima de pedido)
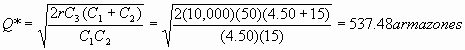
¿Cuál es el nivel máximo de inventario?
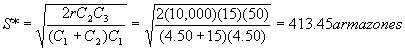
¿Cuál es la escasez máxima que se presentara?
Esto se puede resolver de 2 formas
Forma 1:
Carencia máxima = Q* - S* = 573.48 – 413.45 = 124.03 armazones
O bien
Forma 2:
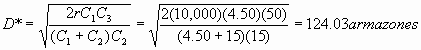
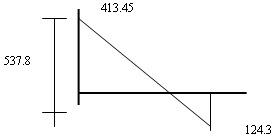
Paso 4: Conclusión
Entonces la carencia máxima que se presentará será 124.03 armazones y cada pedido debe ser 537 o 538 armazones. Se tendrá un nivel máximo de existencias de 413.45 armazones
2 .Compra de disquetes. Una empresa local de contaduría en Guatemala pide cajas de 10 disquetes a un almacén en la Ciudad . El precio por caja que cobra el almacén depende del número de cajas que se le compren (ver tabla). La empresa de contadores utiliza 10,000 disquetes por año. El costo de hacer un pedido es 100 dólares. El único costo de almacenamiento es el costo de oportunidad de capital, que se supone 20% por año. P1=50 dólares, P2=40 dólares, P3=48.50 dólares
Número de cajas pedidas (q) | Precio por caja (dólares) |
0£ q<100 | 50.00 |
100£ q<300 | 49.00 |
q³ 300 | 48.50 |
Cada vez que se hace un pedido de disquetes ¿Cuántas cajas se deben pedir? ¿Cuántos pedidos se hacen al año? ¿Cuál es el costo anual total para cumplir con la demanda de disquetes por parte de la empresa de contadores?
Solución:
Demanda = 10,000 disquetes por año, pero los precios son por caja y sabemos que 10 disquetes trae una caja por lo tanto la demanda es de 1,000 cajas por año.
r=1,000 cajas/año
Costo de ordenar =C3=$100
Costo de almacenamiento = C1 = 0.20 del valor del inventario
C1=0.20Px : Px=P1, P2, P3...Pn
Por lo regular el costo de almacenar en este modelo se da en porcentaje del inventario ya que el precio varia de acuerdo a la cantidad pedida.
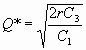
Teniendo estos Q* optimos miro si se encuentran en el rango de la tabla
Q1*=141.42 0£ q<100 X No cumple
Q2*=142.86 100£ q<300 / Si cumple
Q3*=143.59 q³ 300 / Si cumple y Nuevo Q*3=300
¿Por qué si cumple Q*3 y No Q*1?
En Q*1 no puedo menos de lo que necesito por ejemplo no puedo pedir 100 ya que faltarían 42, al contrario de Q*3 donde si puedo pedir mas de 143 y pido 300 ya que es el mínimo que me permite ese precio y el nuevo Q*3 seria 300.
Encuentro los Costo Totales:
El costo 1 se valuó dado que el Q* no cumple.
Conclusión:
Se incurre en menor costo anual el hacer un pedido optimo de 300 cajas, con un costo de $50,288.33/año ordenando 1,000/300=3.33 » 4 veces al año para satisfacer la demanda.
3. Un gran productor de medicina para los nervios produce sus provisiones en remesas, el costo de preparación para cada remese es de $750. De la producción se obtiene 48 galones diarios del producto y cuesta $0.05 cada uno para conservarlos en existencia. La demanda constante es de 600 galones al mes. Suponga 12 meses, 300 días al año y 25 días al mes. Encuentre la cantidad optima de producción, el tiempo de ciclo óptimo, la existencia máxima, la duración en días de cada remesa de producción y el costo total óptimo.
Solución:
Tamaño económico de lote, ciclo productivo, sin faltantes permitidos.
C3= Costo de producción = $750
C1= Costo de almacenamiento = $0.05 /mes
K= tasa de producción = 48 gal/día x 25 días = 1,200 galones / mes
r = demanda = 600 gal /mes
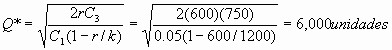
Se podría trabajar en días / meses / años / semanas etc y Q* siempre tiene que dar los mismo, siempre y cuando se utilicen las mismas unidades .
Busco Existencia máxima
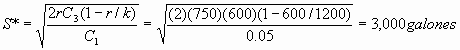
Producción Q*/K = 6,000gal/1,200 gal/mes =5 meses
Tciclo= Q*/r =6,000ga/600 gal/mes= 10 meses
Produce=5/10=0.5 del tiempo 0.5(300)=150 días/año
Se puede utilizar cualquiera de las 2 formulas y da lo mismo para Q*
4. Una empresa de limpieza industrial ha estimado una demanda anual de 50,000 guantes, se estima que existe un costo de ruptura o escasez de Q0.30 unidad/mes se debe analizar la forma de programar lotes de producción si se desean utilizar los recursos minimizando los costos. El costo de mantener el inventario es de Q0.20 unidad/mes, el costo de emitir un lote es de Q150.00. Cual debería de ser la política de la siguiente empresa y la carencia máxima que se le presentara.
Solución:
Tamaño económico del lote reabastecimiento instantáneo faltantes permitidos.
r= demanda = 50,000/año
C2= costo de escasez Q0.30 unidad/mes x 12 meses = Q3.60 unidad /año
C1= costo de inventario = Q0.20 unidad/mes x 12 meses = Q2.40 unidad/año
C3= costo de ordenar = Q150.00
Nótese que el costo de almacenar (C1) se dan directamente como un valor fijo. (en este problema)
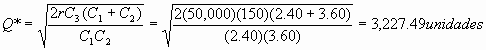
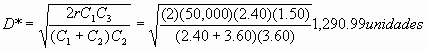
D*=Q*-S* : D*= carencia máxima
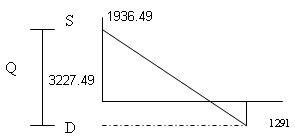
Conclusión: La empresa debería pedir 3,227 o 3,228 unidades cada vez que haga un pedido. Su carencia máxima será de 1,291 unidades.
5. Una constructora debe abastecerse de 150 sacas de cemento por día , la capacidad de producción de la máquina en la empresa es de 250 sacos al día, se incurre en un costo de $400.00 cada vez que se realiza una corrida de producción, el costo de almacenamiento es de $0.5 unidad por día, y cuando hace falta materia prima existe una perdida de $0.7 unidad por día. a) Cuál seria la cantidad optima a pedir. b) La escasez máxima que se presenta .
Solución:
Tamaño económico de lote, ciclo productivo, faltantes permitidos.
r = 150 sacos/día
C3=$400
C1=$0.5 /día
C2=$0.7 /día
a)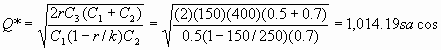 
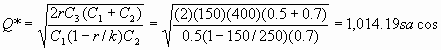
b)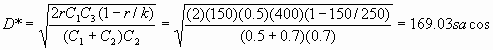 
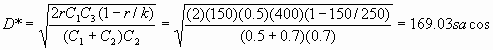
Conclusión: La cantidad optima a producir seria de 1,014 o 1,015 sacos por corrida presentándose una escasez máxima de 169 sacos.
6. Una empresa de informática se dedica a la venta de computadoras, trata de determinar como minimizar los costos anuales relacionados con la compra de tarjetas de video para las computadoras , cada vez que se hace un pedido se incurre en un costo de $20. El precio por tarjeta de video depende del número de tarjetas pedidas según la siguiente tabla
No. de tarjetas pedidas de | Precio por tarjetas de video |
Q<300 | $10 |
300£ q<500 | $9.80 |
Q³ 500 | $9.70 |
El costo anual de almacenamiento es el 20% del valor del inventario. Cada mes la empresa de consultaría emplea 80 tarjetas de video.
POR OTRA PARTE la empresa de informática esta pensando producir las tarjetas de video como otros componentes que ya fábrica. Ocupa a un empleado que trabaja 4 horas y gana $3/hora y a una secretaria para realizar las llamadas la cual trabaja 1 hora y gana $3/hora más un tiempo muerto de la máquina que se valora en $20.
El costo por almacenar la tarjetas es de $1.95/año, la empresa puede producir a un ritmo de 100 tarjetas de video al mes y el precio de cada tarjeta producida sale en $9.85.
Se le contrata a usted como Ingeniero para que determine cual es la mejor decisión que minimice los costos para la empresa. ¿Debería la empresa comprar las tarjetas o producirlas?
Solución:
Analizo descuentos por volumen
C3=$20 (costo por ordenar)
C1=0.20*valor del inventario = 0.20p /año p: precio
r = 80 tarjetas/año = 960 tarjetas / año
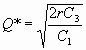
Miro que Q* si estan en el rango y si son validos o no.
Q*1= 138.56 < 300 SI Q1*=138.56
Q*2= 300 £ 139.97 < 500 NO pero cumplo con los 139.97 no importando que sobre y Q2*=300 (nuevo)
Q*3= 140.69 ³ 500 NO también se cumple lo requerido y el Nuevo Q*3=500
Por lo tanto los tres Q* son validos de las siguiente manera
Q*1=138.56 Q*2=300 Q*3=500
Obtengo costos totales
Por lo tanto para la parte de descuento por volumen conviene pedir 300 tarjetas cada vez
Que se le pide al proveedor con un costo anual de $9,766
Análisis para la parte de producir
C1=$1.95 /año (costo de almacenar)
r = 960/año (demanda)
k = 100/ mes =1200 /año (tasa de producción)
C3= costo de ordenar en este caso costo de producir
4 horas 1 empleado y gana $3/hora = $12
1 hora 1 secretaria $3/hora = $3
Tiempo muerto = $20
Total $35
Costo de producir = C3 = $35 por corrida
p= $9.85 (precio de tarjeta)
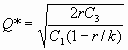
Conclusión:
Al producir el producto la empresa incurrirá en un gasto menor. Lo gastado en descuentos por
volumen seria $9,766/año y al producir seria $9,617.89 y existiría una reducción en
$148.11/año. Por lo tanto esta empresa debería producir las tarjetas de video.
7. Una compañía se abastece actualmente de cierto producto solicitando una cantidad suficiente
para satisfacer la demanda de un mes. La demanda anual del artículo es de 1500 unidades. Se estima que cada vez que hace un pedido se incurre en un costo de $20. el costo de
almacenamiento por inventario unitario por mes es de $2 y no se admite escasez.
- Determinar la cantidad de pedido optima y el tiempo
entre pedidos - Determinar la diferencia de costos de inventarios anuales entre la
política optima y la política actual, de solicitar un abastecimiento de un mes 12 veces al año.
Solución:
r = 1500 unidades/año
C3 =$20
C1 =$2 unidad/mes = $24 unidad/año
T=Q*/r = 50/1500 = 1/30 año x 360 días/año = 12 días
Política Actual se le agota cada mes o sea 1/12 año
1/12=Q*/1500 Q*=125 (política actual)
Política Optima
Q*= 50
Diferencia de $540 por lo tanto se ahora más cuando existe la política optima.
8. Una ferretería tiene que abastecer a sus clientes con 30 sacas de cemento a sus clientes con 30 sacaos de cemento diarios siendo esta una demanda conocida. Si la ferretería falla en la entrega del producto pierde definitivamente el negocio, para que esto no suceda se asume que no existirá escasez. El costo de almacenamiento por unidad de tiempo es de Q0.35 unidad al mes y el costo por hacer el pedido es de Q55.00 a) Cuál es la cantidad optima a pedir b)El periodo de agotamiento (asumir 1 mes = 30 días, 1 año = 360 días)
Solución:
r = 30 sacos / día C1= 0.35 unidad / mes
r = 900 sacos / mes C3= Q55
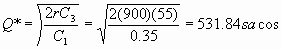
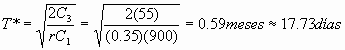ó T=531.84/30 = 17.73días9.Un agente de Mercedes Benz debe pagar $20,000 por cada automóvil que compra. El costo anual de almacenamiento se calcula en 25% del valor del inventario. El agente vende un promedio de 500 automóviles al año. Cree que la demanda se acumula, pero calcula que si carece de un automóvil durante un año, perderá ganancias futuras por $20,000. Cada vez que coloca un pedido de automóviles, sus costos suman $10,000. a) Determine la política óptima de pedidos del agente b) ¿Cuál es la escasez máxima que se presentará?
p = $20,000 p: precio
C1=0.25xvalor del inventario = 0.25p C1=0.25(20,000)=$5,000
C2=$20,000 / año
C3=$10,000
r = 500 / año
carencia máxima
(nivel máximo de inventario)# pedidos = 500/50 = 10 pedidos al año.
CT= Costo de almacenar + Costo de ordenar + Costo de escasez
10.Una empresa industrial utiliza anualmente 10.000 envases para uno de sus productos. Cada envase tiene un precio de 0,50 u.m./unidad, siendo su coste anual de mantenimiento de 0,15 u.m./unidad. Cursar un pedido cuesta, como término medio, 3 u.m., y tarda en ser servido 10 días. Sabiendo que el coste del capital de la empresa es del 15 por 100, se pide:
a) El lote económico de pedido b) El plazo de reaprovisionamiento c) El punto de pedido d) El coste total asociado a los inventarios e) Si el proveedor ofrece un 2 por 100 de descuento sobre el precio por una compra igual o superior a las 600 unidades, ¿qué cantidad interesa comprar cada vez?
SOLUCION:
a) El lote económico de pedido lo calcularemos a partir de la fórmula del modelo de Wilson, en la que llamamos:
C : Consumo anual = 10.000 unidades P : Precio = 0,50 u.m./u.f. A : Coste de mantenimiento anual = 0,15 u.m. S : Coste de emisión de cada pedido = 3 u.m. i : Coste del capital = 15 % t : Plazo de entrega = 10 días
El lote económico de pedido se obtiene de la expresión:
b) El plazo de reaprovisionamiento o días que transcurren entre cada pedido, conocido el consumo anual, se obtiene de:
c) Si el plazo de entrega es de 10 días, el punto de pedido o cantidad existente en almacén que indica la necesidad de cursar un nuevo pedido, será la cantidad necesaria para consumir durante los 10 días que tarda en llegar el pedido; como el consumo diario es de 27,4 u.f.:
d) El coste total asociado a los inventarios será la suma de los costes parciales relativos al aprovisionamiento, esto es:
- Coste de adquisición = P × C - Coste de renovación o reaprovisionamiento = S×(C/Q) es decir, el coste de preparación de cada pedido por el número de pedidos que se cursan al año - Coste de almacenamiento = (A + Pi) × Q/2
Luego el coste total del aprovisionamiento será:
e) Si nos aplican un descuento del 2 por 100 sobre el precio por una compra igual o superior a 600 u.f., nuestro nuevo precio será en este caso:
El coste total para esta nueva consideración será:
Vemos pues que nos interesa más comprar 600 u.f. al precio de 0,49 u.m./u.f., ya que el coste es menor que si compramos 516 u.f. a 0,50 u.m./u.f. (5.017 < 5.115).
11.Una empresa vende un articulo que tiene una demanda de 18, 000 unidades por año, su costo de almacenamiento por unidad es de $ 1.20 por año y el costo de ordenar una compra es de $ 400.00. El costo unitario del articulo es $ 1.00. No se permite faltante de unidades y su tasa de reemplazo es instantánea. Determinar:
La cantidad optima pedida | |
El costo total por año | |
El numero de pedidos por año | |
El tiempo entre pedidos |
Datos
C1= $ 1.00
C2 = $ 400.00
C3 = $ 1.20
La cantidad optima a pedir se calcula de la siguiente forma.
= 3 465 UnidadesEl costo total estará determinado por:
Costo = [(1)(18000)] + [ (400)(18000/3465)] + [(1.2)(3465/2)] = $ 22, 156 por año
El numero de pedidos por año es
N = D / Q = 18 000 / 3465 = 5.2 Pedidos por año
El tiempo entre pedidos es
t = Q / D = 3465 / 18000 = 0.1925 años
12. Una empresa vende un articulo que tiene una demanda de 18, 000 unidades por año, su costo de almacenamiento por unidad es de $ 1.20 por año y el costo de ordenar una compra es de $ 400.00. El costo unitario del articulo es $ 1.00. El costo por unidad de faltante es de $ 5.00 por año. Determinar:
La cantidad optima pedida | |
El costo total por año | |
El numero de pedidos por año | |
El tiempo entre pedidos |
Datos
C1= $ 1.00
C2 = $ 400.00
C3 = $ 1.20
C4 = $ 5.00
La cantidad optima a pedir se calcula de la siguiente forma.
= 3 465 UnidadesEl costo total estará determinado por:
= 747 Unidades 
El numero de pedidos por año es
= 4.66El tiempo entre pedidos es
=0.21513. La demanda de un articulo de una determinada compañía es de 18, 000 unidades por año y la compañía puede producir ese articulo a una tasa de 3 000 unidades por mes, El costo de organizar una tanda de producción es $ 500.00 y el costo de almacenamiento de una unidad es de $ 0.15 por mes. Determinar la cantidad optima de debe de manufacturarse y el costo total por año suponiendo que el costo de una unidad es de $ 2.00,
= 4 470 UnidadesEl costo total anual es
= $ 40, 026El inventario máximo estaría determinado por:
= 2 235 Unidades14. La demanda de un articulo de una determinada compañía es de 18, 000 unidades por año y la compañía puede producir ese articulo a una tasa de 3 000 unidades por mes, El costo de organizar una tanda de producción es $ 500.00 y el costo de almacenamiento de una unidad es de $ 0.15 por mes. Determinar la cantidad optima de debe de manufacturarse y el costo total por año suponiendo que el costo de una unidad es de $ 2.00. El costo por unidad agotada es de $ 20.00 por año.
Datos
D = 18, 000 Unidades por año
R = 3,000 por mes
C1 = $ 2.00
C2 = $ 500.00
C3 = $ 0.15 por mes
C4 = $ 20.00 por año
La cantidad optima estará definida por:
= 4670 Unidades Para calcular el costo anual primero se deben calcular el numero de unidades agotadas.
= 193 UnidadesEl costo total quedara definido por
Costo Total = $ 39, 855 por periodo de planeación.
15. Un agente de mercedes benz debe pagar 20 000 dólares por cada automóvil que compra , el costo anual de almacenamiento es de 25% del valor del automóvil , el agente vende 500 autos al año su costo por faltantes sera de 20000 dólares. Cada vez que el agente coloca un pedido su costo es de 10 000 dólares determine:
- La cantidad que debe ordenar el cada pedido Q
- El máximo nivel de inventario.
- el numero de ordenes por año
- El costo mínimo anual.
16. Si la demanda de un artículo es constante de 9000 unidades / año el costo a ordenar es de 2.5 dólares /orden y el costo de conservación es de 2 dólares por unidad al año.
- Encuentre el tamaño del lote económico.
- Número de ordenes por año.
- Cada cuanto tiempo llega un pedido.
- Cual es el costo del inventario anual.
- Cual es el punto de reorden si el tiempo de entrega es de 3 días.
17. Una Cía. fabricante de refrescos a observado que requiere anualmente de 3000 baleros que son utilizados en las bombas de agua con un programa de mantenimiento preventivo diseñado por el departamento de producción. El costo de cada unidad es de $ 80,000 , el costo de oportunidad de inversión es de 12% del costo del producto. Los costos generados por el control de inventarios como son el sueldo de personal de almacén, agua y electricidad es de 2,400 * unidad , otro costo que representa aun los deterioros , extravió y envejecimiento de los productos almacenados anualmente y alcanzan un costo de $2,000 * unidad .La orden de compra se ha estimado en $120,000 .
Suponga que el proveedor tarda en promedio 15 días en surtir una orden, determinar :
El tamaño económico del lote.
El inventario máximo.
El inventario Promedio.
El punto de reorden.
El tiempo requerido para consumir el inventario máximo.
Costo total del inventario.
Número de pedidos.
Datos:
D = 3000 unidad por año.
Ci = $80,000
Co =$120,000
Ch= 0.12 (80,000)+ 2,900 + 2,000
Ch = 14,000 unidades por año.
L = 15 días .
18. Frecuentemente un gerente de producción desea tomar la producción , ya sea de comprar o manufacturar un articulo. Los modelos vistos hasta el momento pueden ser usados para tomar tal decisión.
Suponga que un artículo puede ser comprado a $25 la unidad o fabricado a un tasa de producción de 10,000 unidades por año, con un costo de $22 la unidad. Sin embargo si lo compramos el costo de una orden es de 45 mientras que el costo de organizar una tanda de producción. (preparar el equipo) es de $50. La demanda es de 2,500 unidades por año, el costo de conservar el inventario es de 10% del costo del producto. Determinar que es preferible, si comprar o manufacturar.
Comprar
Ci = $25 u.
Co= $5
Ch = 0.10(25) = $2.5
D = 2,500 u / año.
Ct = $ 62,750
Manufacturar
S = 10,000 u / año.
Ci = $22 unidades.
Co =$50
D = 2,500 u / año.
Ch = 0.10 (22) = $2.2
Ct = 55,692
De acuerdo con los costos obtenidos conviene mejor manufacturar el producto que comprarlo.
Una vez que el gerente ha decidido fabricar el producto desea conocer también:
- El inventario máximo.
- El tiempo de producción.
- El punto de reorden (una orden tarda 1 semana en atenderse).
- El tiempo de ciclo.
- El tiempo en que no existe producción y que no se puede ocupar para dar mantenimiento a las maquinas.
- El inventario promedio.
- El número de ordenes de fabricación.
19. Un impresor que en la actualidad esta haciendo una compra mensual, estudio el comportamiento del papel libro de 70 gr. en los últimos doce meses, encontró que su demanda fue de: 10, 11, 10, 9, 10, 11, 9, 10.5, 10, 9, 9 y 11.5 toneladas por mes, estima el precio de compra se va a mantener en $2.300.000 por tonelada, su costo de pedido en $500.000 y por política carga un 15% del costo unitario al manejo de los inventarios mas $55.000 por concepto de bodegaje, calcular:
1. El modelo a manejar en estas condiciones.
1. El modelo a manejar en estas condiciones.
Lo primero que debemos observar es el comportamiento de la demanda el cual vemos que es relativamente constante, por lo que podemos asumir que nuestro modelo se comporta de acuerdo a los parámetros de un modelo de cantidad económica de pedido con los siguientes datos de entrada:
D = 120 toneladas año
Co = $500.000
C = $2.300.000 tonelada
Cc = $400.000 tonelada/año
Por tanto
D = 120 toneladas año
Co = $500.000
C = $2.300.000 tonelada
Cc = $400.000 tonelada/año
Por tanto
Como podemos observar en esta política de compra de inventarios, la empresa ahorra más de un 20% en el costo asociado a los inventarios que tendría si efectuase una compra mensual ( CA = 12*500.000 + [12/2]*400.000 = $8.500.000), lo que sumado al ahorro que se lograría con los diferentes productos que maneja la compañía permitirá mejoras importantes en la rentabilidad al final del ejercicio.
20. Una compañía de taxis consume gasolina a una tasa de 8500 galones/mes. La gasolina cuesta 1.05$/galón y tiene un coste de emisión de pedido de 1000$/pedido. El coste de mantener el inventario es 1 centavo/galón/mes.
a) Determine cuándo y cuánto se debe ordenar, si desea minimizar el coste total.
b) Suponga que se permiten roturas de stock, y que éste asciende a 50 centavos/galón/mes.
c) Suponga que el coste de la gasolina baja a 1$/galón si compran, al menos, 50000 galones.
d) Suponga que el coste de la gasolina es 1.20$/galón si el tamaño del pedido es menor de 20000galones, 1.10$/galón si a2=40000 galones, y 1.00$/galón si Q es, como mínimo, 40000 galones.
e) ¿Es necesario el dato de q para resolver este problema?
SOLUCION:
Apartado a:
Q*= 41231 galones.
Frecuencia (nº de pedidos al mes): 0,21 ; Frecuencia (nº de pedidos al año): 2,47
T* (meses)= 4,85 ; T* (días) = 146
Apartado b:
Q* = 41641 galones
Frecuencia (nº de pedidos al mes): 0,20 ; Frecuencia (nº de pedidos al año) = 2,45
T* (meses)= 4,90 ; T* (días) = 147
Apartado c:
Q1* = 41231 galones
Q2* = 42249 galones
CT(Q1*) = 9337 $
CT(a) = 8908 $
Q*= a = 50000 galones
Frecuencia (nº de pedidos al mes): 0,17 ; Frecuencia (nº de pedidos al año) = 2,04
T* (meses): 5,88 ; T* (días): 176
Apartado d:
Q1* = 38568 galones
Q2* = 40283 galones
Q3* = 42249 galones
SITUACIÓN: a1<Q1*<a2<Q2*<Q3* Þ Q*=Q3*=42249 galones
Frecuencia (nº de pedidos al mes): 0,20 ; Frecuencia (nº de pedidos al año) = 2,41
T* (meses)= 4,97 ; T* (días) = 149
